A linear element, or a lower order element is characterized by a linear shape function. The displacements of the mesh region between the nodes vary linearly with the distance between the nodes. Linear elements do not capture bending.
A quadratic element, or a higher order element utilizes a non-linear shape function. The displacements between the nodes are interpolated using a higher order polynomial. These elements have mid-side nodes – An element edge would consist of three nodes instead of two. Quadratic elements are better suited to represent complex geometries and bending deformations.
Quadratic elements are computationally more expensive than linear elements.
Lower order tetrahedral elements will make the model overly stiff and should be generally avoided.

The image below shows another comparison of linear and quadratic element order:
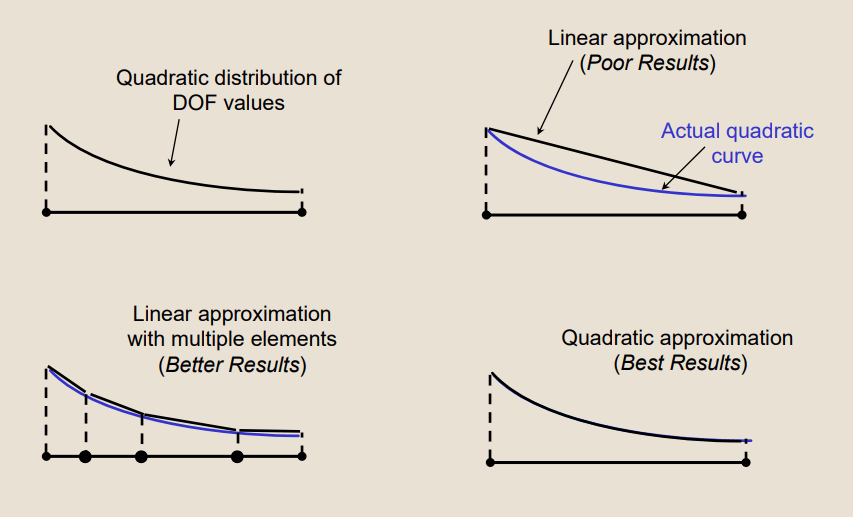
The differences between Linear and Quadratic elements are summarized in the table below:
| Linear Elements | Quadratic Elements |
| Linear Shape Function | Quadratic Shape function |
| Mostly constant state of stress within a single element | Linear variation of stress within a single element |
| Cannot represent curved edges and surfaces accurately | Can represent curved edges and surfaces accurately |
| Highly sensitive to element distortion | Relatively less sensitive to element distortion |
| Generally only acceptable if you are only interested in nominal stress results | Recommended if you are interested in accurate stress distribution |
| Need to use a large number elements to resolve high stress gradients | Give better results than linear elements, often with fewer elements |
| Generally, computationally less expensive (simulation runs fast) | Generally, computationally more expensive |