In general, the finer the finite element mesh, the more accurately one can capture the contours of a geometry and there are more “data points” on the geometry to generate an accurate displacement and stress response.
A mesh independence (or grid independence) study is something an analyst can perform to determine the dependence of the results on the mesh density. One of the ways this can be done is by following the approach listed below. There are other ways to directly check the mesh quality using mesh quality metrics, as described here.
- Isolate an area of interest on the geometry. If the model is small, this could be the whole geometry. But usually, this is is not practical so one could focus on a specific region of the geometry.
- Determine a method to quantify the nodes on the area of interest. This could be done by getting the node count on a radius, chamfer, body, or a named selection.
- Refine the mesh in the are of interest. A few best practices should be used when refining the mesh. These are listed below:
- Only change the mesh sizing. Do not change any other mesh setting such as element type or order. This will ensure a fair comparison between the runs.
- Ensure that the increase in mesh count between two runs is “significant”. By significant we imply a minimum of 10%. This percentage is a guide based on experience and judgment.
- Obtain at least three different meshes. Two meshes may be sufficient to prove mesh independence. But for relatively coarse starting meshes, one would typically need three or more runs to establish mesh independence.
- Choose a result to study. Typically, this would be a stress value. It could be an equivalent stress such as von-Mises, a stress component or one of the principal stresses. One may also choose some other result (plastic strain, accumulated damage, fatigue life etc.) depending on the scenario.
- Compare the results for the various runs. One can plot the number of nodes vs the stress, and look for a point where a significant increase in node count does not result in a significant increase in stress. The analyst may plot raw data, percentages, or both.
The figure below shows an example of a mesh independence plots. It can be seen that a minimum of 5,000 nodes is required to get a mesh independent stress. This stress is 690 MPa.
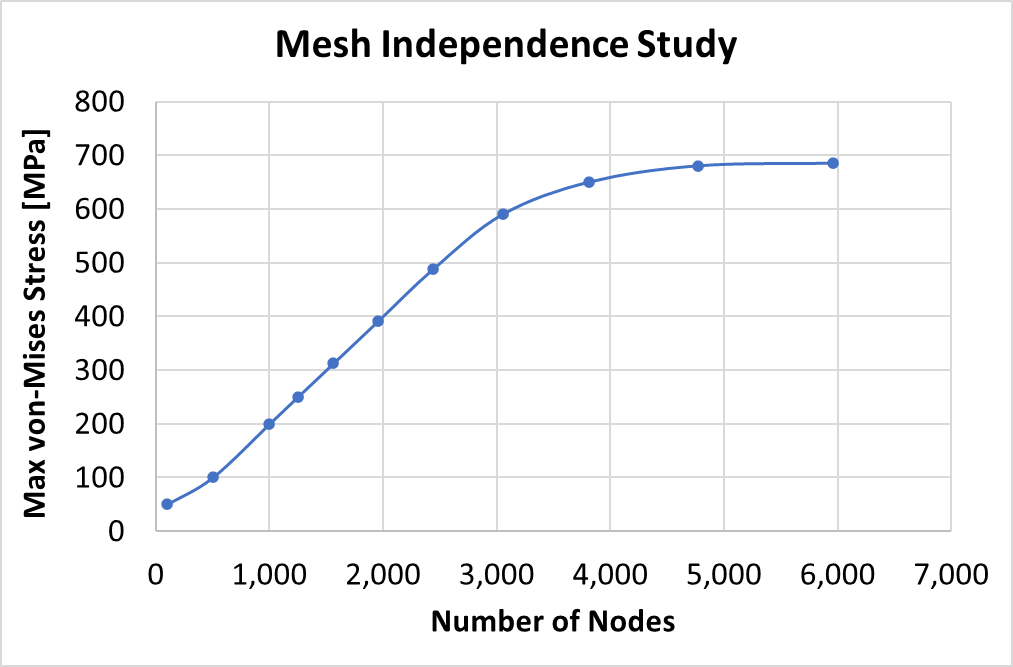
It is typical for models with coarse meshes to under report the stress values. In some rare cases the opposite may be true. We will discuss the mechanism by which stresses vary with meshes in another post.
If you found this article useful, you may be interested in our eBook on FEA.
