Internal and external forces are often mentioned in the context of structural analysis. For example, an FEA solver converges to a mathematical solution by comparing the external and internal forces acting on a body.
In term of structural analysis, external forces are the input loads. This can be any type of load acting on a body such as dead weight, pressure, point loads, etc.
Internal forces are generated within the structure of the body, as a response to the external forces (Newton’s Third Law of Motion: Every action has an equal and opposite reaction).
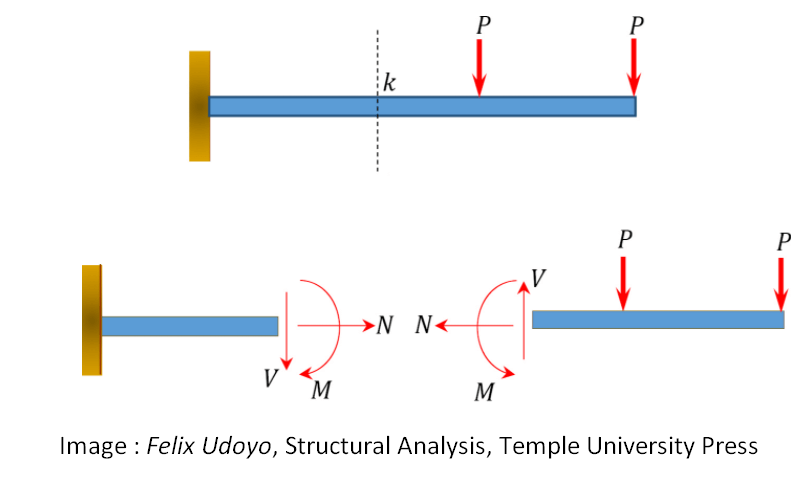
It is because of the internal forces that the body is able to sustain the external loads and remain in equilibrium. Consider the cantilever beam shown below.
If we imagine a cross-section of the beam at k, we will end up with two sides of the beam. Each side will have a “cut-face”. We know that the right-hand side must cancel out the effect of the two point loads (P) in order to remain in equilibrium. We can represent the load reactions acting on this cut-surfaces by a shear force (V), a normal force (N) and a bending moment (M). These are the internal forces acting on this cross-section.
We also know that the cut-face on the left side must not move relative to the cut-face on the right in any DOF (Degree of Freedom). In order for this to happen, equal and opposite internal forces must also act on this cut surface.
It is this principal of balancing the internal and external forces which lies at the heart of structural analysis.