Load Controlled vs Displacement Controlled Models – Which one to use in FEA?

Introduction

In this article we will discuss some aspects of load and displacement controlled models. We will look at what we mean by these terms, and relate our understanding to Finite Element Analysis.

What do we mean by load or displacement control?

When we perform a scientific experiment or a test, we are usually studying a system of cause and effect. We are interested in the effect of varying one variable on another. What we vary, or control is called the independent variable. What we are measuring, is the dependent variable. In other words, in a load controlled test, the load is the independent variable (and displacement is the dependent variable). In a displacement control test, the displacement is the independent variable (and the load reaction is the dependent variable).

Shouldn’t the two be interchangeable?

At first thought one might think that load controlled or displacement controlled tests should result in identical, or at least very similar system responses. However, this is not always true. To illustrate this, we shall take a common and simple real-word example: uniaxial tensile testing.

It is well known that tensile testing is used to generate material stress-strain curves. Typically, the tensile testing employed for determining material stress-strain curves is strain controlled (this is analogous to displacement control since strain is the ratio of displacement of a volume to its original length). The tensile stress experienced by the test specimen is measured as a function of the applied strain, and a curve similar to the one shown below is generated. This image represents a typical polymer stress-strain curve [Ref 1].

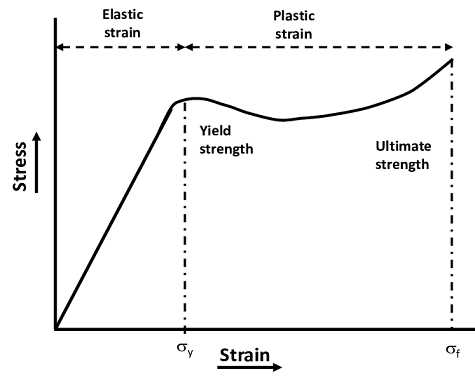
If the same curve was generated using the data from a stress controlled test (this is analogous to load controlled since stress is force distributed over an area), we would get what is shown in the dotted line in the figure below between points A and B. The dotted line represents where the stress controlled test will deviate in response from the strain controlled test.

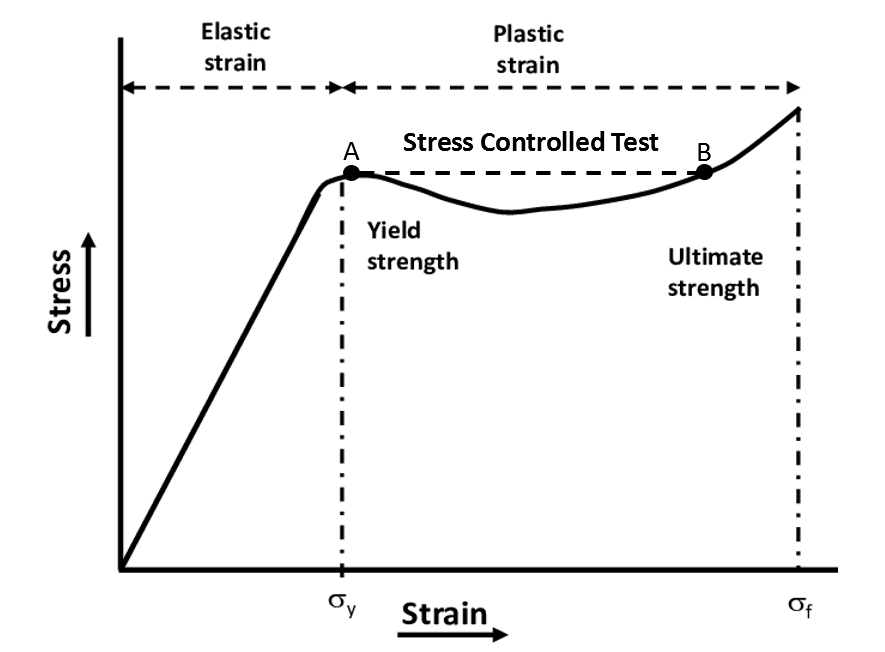
For a stress controlled test, the stress being the independent variable, continues to increase incrementally and can only increase with time. This means that the response that we plot is a step function between A and B, whereas with a strain controlled test, a reduction in stress was observed as the strain increased.

Check out FEA Tips eBook – All Models are Wrong

Which method is more commonly employed in structural FEM?

A structural FEM essentially solves the system of equations: [K]{u} = {F} where [K] is the stiffness matrix, {u} is the nodal vector and {F} is the Force Vector. Here, the dependent variable is {u} and the independent variable is {F} – which implies that the system of equations represents a load controlled situation.

The majority of real world problems are better understood and represented via load control. Components are generally exposed to a variety of loads, all of which eventually manifest themselves as stress and strain – Force, pressure, acceleration, temperature gradients and electromagnetic loads all result in displacements of the component and generate stresses.

Because of the above, it is generally advisable to use a load controlled approach in FEM. In many instances, it is impossible to model a real life combined loading situation accurately using a displacement controlled model, because one cannot predict the displacements beforehand.

Employing a load controlled method in FEM means that the loads are used as independent variables – We use forces, pressures, temperatures etc. as inputs to the model. The displacements generated are a result of the input loads.

When is it desirable to use displacement control in FEM?

There are many instance where using displacement control is the preferred method. By displacement control, we mean that in the FE model we apply displacements (at selected nodes) as the independent variable. The reaction forces generated by the model represent the forces and moments corresponding to the applied displacements.

1. To better represent the real world physics. For example:
   
   • Simulation of a uniaxial tension test as discussed earlier.
     
   • Metal forming processes such as rolling, bending and extruding where metals are plastically deformed into desirable shapes.
     
   • An elastomeric seal being energized by letting it expand / stretch into a groove in order to create a seal.
     
2. To aid in convergence of the numerical solution. For example:
   
   • The displacements change a lot with small load increments. This is true for all of the situations mentioned under point 1. There may also be other cases, such as when simulating a component to its collapse load – Once a metal exceed its yield point, the material starts to “flow” and numerical stability can only be achieved if this flow is manually controlled via a displacement control model.
     
   • When load control results in a singular stiffness matrix. This means that the FE model is poorly defined and one of more components can undergo rigid bod motion. This may happen if some components are only prevented by contacts from flying off in space. In such situation displacement control or a hybrid of displacement / load control may work best.

A “hybrid” of load and displacement is often the best choice

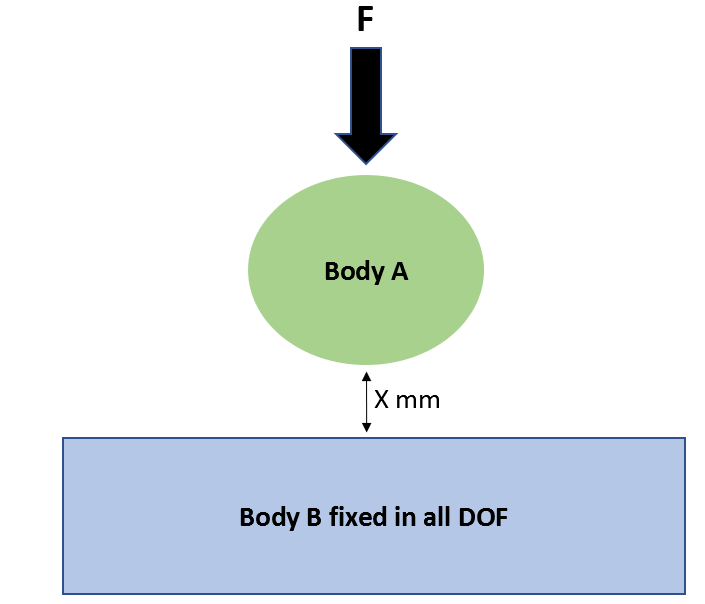
This can be clarified with an example. Consider the system represented by the two bodies in the image below. A force F is to be applied to body A till it displaces X mm, makes contact with a surface and then gets compressed by the force. If the force F is applied in a load controlled model, the displacing body will undergo rigid body motion, making it difficult to converge. This may be true even if the body is constrained in the other two directions.

One way to remedy this is to break up the analysis into multiple steps – In the first step a displacement x is applied to body A instead of Force F such that contact between body A and B is established. At this point (step 2 of the analysis) the Force F is applied to generate the desired response.

Conclusion

Load controlled and displacement controlled models both have their positions and roles in the world of simulation. The most important thing is to consider the physics that is being modelled and start with the method which most closely represents real life.

• In some situations both model types are acceptable and generate comparable results.
• Sometimes the choice of the type of model is critical in determining the system response accurately.
• In some scenarios displacement control may offer model stability with acceptable loss of accuracy in determining the system response.
• In some instances hybrid models may be the best approach where an initial displacement control is applied for stability followed by load control to simulate the physics accurately.

If you found this article useful, you may be interested in our eBook on FEA.

References

[1] John H, Campbell, Three-dimensional printing and deformation behavior of low-density target structures by two-photon polymerization