How is the yield strength of a material determined?
The yield strength of most materials is something that can be determined by performing a tensile test in the lab. This typically entails taking a specimen of the material with a known uniform cross section and applying a uniaxial tensile load. A stress-strain plot is typically generated since it provides the information regarding the mechanical behavior of the specimen.
Figure 1 shows a tensile test machine and Figure 2 shows a typical stress-strain curve for metals.

Note that the exact point at which yielding starts (i.e. the slope of the stress-strain curve changes from its initial value) is difficult to determine exactly from figure 2. For this reason, the stress at point 4 is labelled as the yield strength of the material. The 0.2% strain offset is arbitrary, but is a well established industry standard. This value of strain corresponds to a stress level where yielding has already begun.
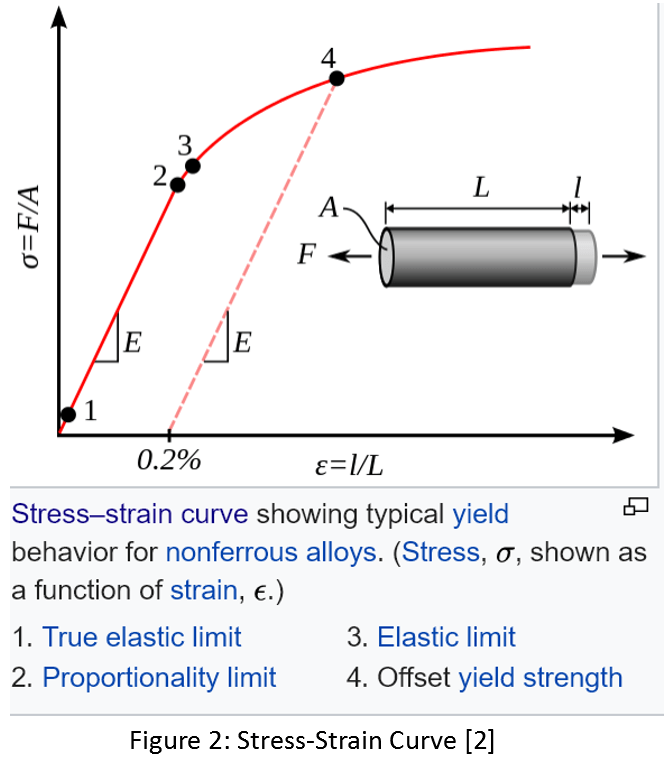
So when someone says that they used a 150 MPa yield strength material, it means that under a uniaxial loading situation, a tensile stress of 150 MPa will cause the material to yield.
Uniaxial is the key word here – More on this below.
What is a failure theory?
The yield strength determined by the method above is for uniaxial loading only. Uniaxial means that there is only one load acting along the axis of the specimen. However, real life loading is usually more complex than this. Components typically see what we call a combined loading situation. You may have a combination of tensile forces, bending moments and torques.
How do we determine what stress causes yielding under a combined loading, or multiaxial loading situation?
This is where Failure Theories, also called Yield Criteria come in.
“A yield criterion can be any descriptive statement that defines conditions under which yielding will occur. It may be expressed in terms of specific quantities, such as the stress state, the strain state, a strain energy quantity, or others.” [3]
What are some of the commonly used failure theories?
Some of the failure theories are:
- Maximum Shear Stress (Tresca)
- Octahedral Shear Stress (Distortion Energy or von-Mises)
- Strain Energy Density
- Maximum Principal Strain
- Maximum Principal Stress
Any intermediate text book on mechanics of materials would give detailed descriptions of the mathematical basis of these theories. One that I can recommend is Advanced Mechanics of Materials, Boresi and Schmidt (Sixth Edition, Chapter 4, Inelastic Material Behavior).
For design purposes, Tresca and von-Mises stress theories are usually employed. This is because robust testing and years of designing has shown that these two theories quite accurately depict the inelastic behavior of real world material and applications. Additionally, Tresca theory is generally more conservative than von-Misses.
A comparison of maximum shear stress and octahedral shear stress failure theories (Tresca vs von-Mises)
The following are some excerpts from SolidWorks help. This is one of the most concise and clear explanations of this topic which I have come across:
Maximum Shear Stress Criterion
The maximum shear stress criterion, also known as Tresca yield criterion, is based on the Maximum Shear stress theory.
This theory predicts failure of a material to occur when the absolute maximum shear stress (τmax ) reaches the stress that causes the material to yield in a simple tension test. The Maximum shear stress criterion is used for ductile materials.
τmax >= σ limit / 2
τmax is the greatest of abs (σ12, σ23, σ13) where:
σ12 = (σ1 – σ2) / 2;
σ23 = (σ2 – σ3 ) / 2;
σ13 = (σ1 – σ3) / 2
σ1, σ2, σ3 are the principal stresses in descending order.
Maximum von-Mises Stress Criterion
The maximum von Mises stress criterion is based on the von Mises-Hencky theory, also known as the Shear-energy theory or the Maximum distortion energy theory. The theory states that a ductile material starts to yield at a location when the von Mises stress becomes equal to the stress limit. In most cases, the yield strength is used as the stress limit.
von-Mises stress can be expressed in various ways, as shown in the table below:

Comparison between Maximum Shear Stress and von-Mises Stress Criteria

The 2D yield surface for von-Mises criterion is larger than that for Tresca as shown in the Figure above implying that the Tresca criterion is more conservative.
It has been observed that for polycrystalline materials (ductile metals), von Mises condition of constant shearing stress intensity in the state of yielding agrees somewhat better, in general, with experimental data. There are other cases, however, that the Tresca-Saint Venant conditions appear to be in better agreement with experimental data. Thus, the two methods may be regarded as equally possible formulations of the yield condition.
- For the states of uniaxial or equibiaxial stress, the two criteria are equivalent.
- At other stress states yielding occurs at lower stress values according to the Tresca conditions; under equal loading conditions, the Tresca criterion predicts larger plastic deformation than the von Mises.
- Maximum deviation between the two models occurs for the state of pure shear. At this stress state, based on the Tresca conditions, yielding occurs at 87% of von Mises stress [5].
References
[1] https://en.wikipedia.org/wiki/Tensile_testing
[2] https://en.wikipedia.org/wiki/Plasticity_(physics)
[3] Advanced Mechanics Of Materials, Boresi, Schmidt, 6th edition, Page 114
[4] https://en.wikipedia.org/wiki/Von_Mises_yield_criterion
[5] SolidWorks Help, Plasticity Models
