Introduction

Seismic loads are often considered in static structural analysis to verify protection against structural failure as a result of an earthquake. In this article, we will provide a brief summary of one of the commonly used methods of accounting for seismic loads in a static structural analysis.

Earthquakes and Vibrations

What happens when a structure experiences an earthquake? Earthquakes develop underground, so naturally they are associated with vibrations of the ground.

Structures that are built on top of the ground will also experience the vibrations. However the response of each structure to these vibrations will vary based on a number of factors.

A structure may exhibit one or more patterns or ways of vibration. For example it may oscillate from side to side, up and down or it may twist.

Each pattern of vibration is called a mode and the specific pattern associated with this mode is called the modal shape. Each mode is also characterized by a frequency (number of complete oscillations per second) called the modal or natural frequency.

“A natural frequency is defined as that frequency at which a body will vibrate if excited by an external force” [1]

When structures vibrate as a result of an earthquake, they vibrate according to one of the modes. This leads us to our first step in our analysis:

Step 1: Perform a Modal Analysis

Now that we know what a mode is, it makes sense for us to determine the modes of the structure that we are studying. For this purpose one would perform a modal analysis. A modal analysis will provide you with the following information:

1. The number of modes associated with the model
2. The modal shape for each mode
3. The modal frequency for each mode
4. The mass participation factor for each mode (See next step)

By now, the first three items are self explanatory. The image below shows an example of a structure with 6 modes and its frequencies as reported by a modal analysis performed with ANSYS.

Step 2: Identify the Dominant Mode(s)

In addition to the modal shapes and frequencies, a modal analysis also generates the mass participation factors. Each mode calculated by the software is associated with a mass participation factor which represents the percentage of system mass contributing to that mode. The higher the number, the more the mass participation and the more kinetic energy associated with that mode. Typically, one would choose the mode(s) with the highest mass participation for further analysis.

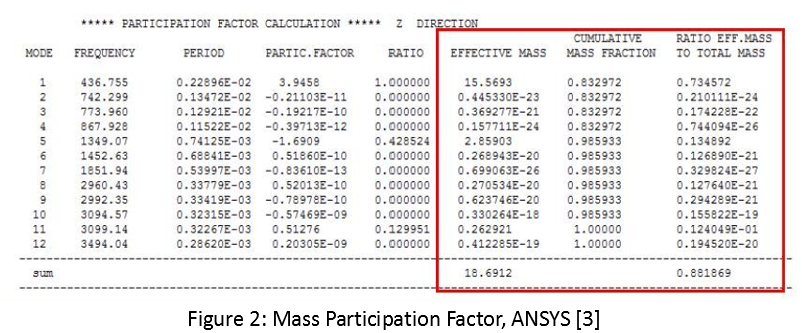
Figure 2 shows a table from an ANSYS modal analysis. Mode 1 is the dominant mode in the Z direction with 83% of the system mass contributing to it.

Step 3 : Obtain a Response Spectrum Plot

A response spectrum is a function of frequency or period, showing the peak response of a simple harmonic oscillator that is subjected to a transient event. The response spectrum is a function of the natural frequency of the oscillator and of its damping. Thus, it is not a direct representation of the frequency content of the excitation (as in a Fourier transform), but rather of the effect that the signal has on a postulated system with a single degree of freedom (SDOF) [6].

The response may be acceleration, velocity or displacement as a function of frequency.

A response spectrum plot corresponding to the geometry in question can be used in two ways: Equivalent Static Load Method or Response Spectrum Analysis. You can use Step 4 or Step

Step 4: Read the Accelerations Corresponding to the Mode Identified in Step 2

Once we have the Response Spectrum plot we can determine the x, y, and z direction response (acceleration, velocity or displacement) values corresponding to the mode identified with the modal analysis. If step 4 is to be used (as opposed to step 5) then it may be ideal that the acceleration response is available since it is easy to apply accelerations in a structural analysis.

Finally, the acceleration values determined through this process can be applied as input loads in a static structural analysis. It should be noted that these accelerations must be input along with a dynamic amplification factor (DAF).

This method is called the Equivalent Static Load Method.

Step 5: Perform a Response Spectrum Analysis

Perform a Response Spectrum Analysis (RSA). This is a method to estimate the peak response of a system based on an input Response Spectrum. A Modal combination procedure is applied to use the results of the modal analysis and the input response spectrum plot to estimate the peak response (displacement / Stress) of the system.

Further Reading

There is a lot of literature available on seismic analysis

One extremely concise and useful book that I can recommend is a publication by NAFEMS (The International Association for the Engineering Modelling, Analysis and Simulation Community) is: How to Do Seismic Analysis Using Finite Elements

From the publisher:

“This book aims to provide practical guidance on the application of FEA to the seismic analysis of structures and equipment, and to inform the reader generally about seismic analysis.

The intended audience is the practicing engineer (and to a lesser degree engineering managers). It is assumed that the reader has some understanding and experience of seismic engineering and FEA.

Examples of actual applications of FEA to safety critical structures and plant are used to illustrate some of the techniques and guidelines given within this document.”

References

[1] William E. Forsthoffer, Forsthoffer’s Best Practice Handbook for Rotating Machinery

[2] Supriya Sahu and B. B. Choudhury, Stress and Modal Analysis of Six-Axis Articulated Robot Using ANSYS

[3] Ansys Training Material, ANSYS Mechanical Linear and Non-Linear Dynamics, March 2011

[4] Michalis Fragiadakis, Response Spectrum Analysis of Structures Subjected to Seismic
Actions, Laboratory for Earthquake Engineering, National Technical University of Athens (N.T.U.A.), Athens, Greece

[5] Ansys Training Material, ANSYS Mechanical Linear and Non-Linear Dynamics, 2019

[6] COSMOL Multiphysics Encyclopedia, Response Spectrum Analysis