In this short article we will define some terms which are commonly used among the scientific and engineering communities to refer to problems and their solutions. Sometimes people use some of these terms casually, or interchangeably which could lead to misunderstandings. Knowing the commonly accepted meanings of these terms can prevent miscommunication.

Analytical Solution is an exact solution to a well defined mathematical problem. This is also called a “closed form solution”. Consider the example of a cantilever beam of length L and a point load P acting at its free end. We know that its deflection at the free end is PL^3 / 3EI.

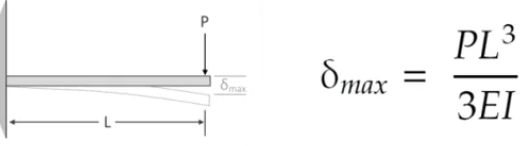
The deflection calculated by this formula is an analytical solution.

Numerical Solution is an approximation of the exact solution. There are various mathematical techniques which can be used to obtain numerical solutions for problems.

The above described cantilever beam can be modeled in a structural analysis software and a Finite Element Analysis may be performed. The maximum deflection reported by the analysis would then be a numerical solution.

Empirical Solution is the same as an experimental solution. It is when you physically test a specimen in the lab, shop or other real world setting. Going back to our cantilever beam example, one could perform a load test on a test beam in a lab and measure the maximum deflection using strain gages or by some other means. This displacement would be an empirical solution.

Why obtain a numerical solution when we can calculate analytical solutions?

The key word in this question is “when”. Indeed, if an exact solution for your problem exists, then there is no need to go through the process of obtaining a solution which is a “mere” approximation. But the truth is, that the vast majority of “real-world” problems can not be solved analytically. There are several reasons for this.

For one, analytical solutions themselves include some assumptions. They are “idealized” solutions. This means that various physical phenomena which would potentially be at work in real life, are ignored in analytical solution – Many times, this is acceptable but in some cases these approximations could limit the accuracy with which one desires the solution to a problem.

Secondly, we may know of some mathematical relationships useful for our problem, but the values of the variables within the equations may not be known. For example, obtaining the value of a displacement due to an applied force from the equation F = kx is only possible if we know the stiffness for our structure (K). How do you define the “stiffness” of a car, a building or a bridge? This is where a numerical solution can come in, approximate the stiffness of the structure and give you a reasonable result.

And finally, the mathematical relationships defining our problem may not be known – which is true for the vast majority of real life scenarios. A numerical scheme can be used to utilized known relationships, and model the response of a structure. Such a result may be verified through empirical processes to establish some set of useful rules.

Often times, a combination of analytical, numerical and empirical solutions is used to qualify a design. By qualify, we mean to verify that the design will maintain its form, fit and and perform its function in a feasible and safe way over the expected life of the design.