Introduction
In this article we will discuss the concept of material plasticity, how plasticity is employed in ANSYS and what are some of the best practices for choosing plasticity models.
What is Plasticity?
In order to define a linear material model in ANSYS, one needs to define the young’s modulus and poison’s ratio. Non-linear material modeling requires that a material plasticity model be chosen, and a stress-strain curve be included as part of the material properties. Material plasticity is indicated by irreversible straining (deformation) of material after a certain stress (load) is reached.
Why is Plasticity Important in Material Modeling?
The yield strength of most metals is something that can be determined by performing a tensile test in a lab. This typically entails taking a specimen of the material with a known uniform cross section and applying a uniaxial tensile force to it. A stress-strain plot is typically generated since it provides the information regarding the mechanical behavior of the specimen. The figure below shows an arbitrary uniaxial stress-strain curve.
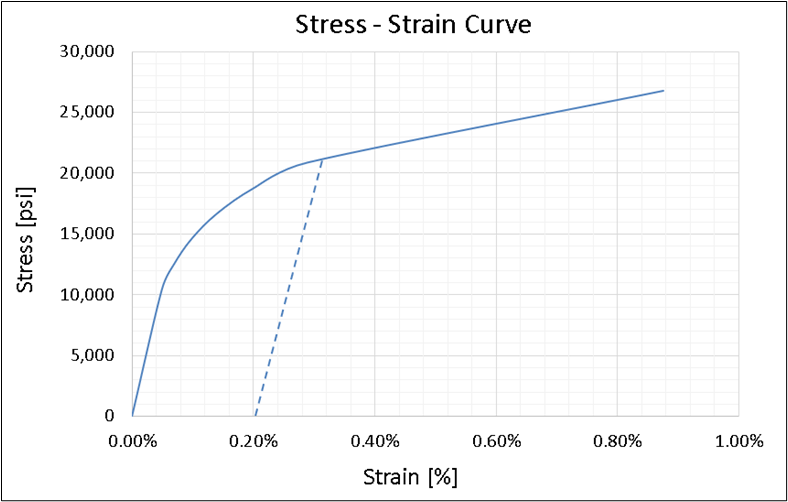
Note that the exact point at which yielding starts (i.e., the slope of the stress-strain curve changes from its initial value) is difficult to determine exactly from Figure 1. The typical practice is to consider the stress corresponding to 0.2% plastic strain as the yield strength (Approximately 21,000 psi in Figure 1). The 0.2% strain offset is arbitrary but is a well-established industry standard. This value of strain corresponds to a stress level where yielding has already begun.
Check out FEA Tips eBook – All Models are Wrong
When someone says that they used a 150 MPa yield strength material, it means that under a uniaxial loading situation, a tensile stress of 150 MPa will cause the material to yield. Uniaxial is the key word here. The yield strength determined by the method above is for uniaxial loading only. Uniaxial means that there is only one load acting along the axis of the specimen. However, real life loading is usually more complex than this. Components typically see what we call a combined loading situation. You may have a combination of tensile forces, bending moments and torques.
How do we determine what stress causes yielding under combined loading, or multiaxial loading situation and how does the plasticity evolve with loading?
This is where the concepts of plasticity modeling come into play.
Rate-dependent vs Rate-Independent Plasticity
Two types of plasticity models are available – Rate-Independent and Rate-dependent.
As the name suggests, for rate-Independent plasticity, the plastic strains are assumed to develop instantaneously and are not a function of time. This is a reasonable assumption for the bulk of engineering problems.
Rate-dependent plasticity models describe the plastic flow of material which is dependent on time or strain rate. These are used in specialized applications, such as thermal creep and metal forming operations.
Rate-Independent Plasticity
Rate-Independent plasticity modeling is described by three constituents:
1) Yield Criterion: “A yield criterion can be any descriptive statement that defines conditions under which yielding will occur. It may be expressed in terms of specific quantities, such as the stress state, the strain state, a strain energy quantity, or others.” [1]
2) Flow Rule: The flow rule determines the direction of flow of the plastic strains. It relates the plastic strain increments to the stress increments after the onset of yielding.
3) Hardening Rule: The hardening rule describes the effect of plastic strain on the strength of the material. More precisely, it predicts the changes in the yield surface (a geometric representation of the yield criterion) due to the development of plastic strain.
Plasticity Models
ANSYS provides several options for plasticity modeling. Some of these are listed below.
- Bilinear Isotropic Hardening (BISO)
- Multilinear Isotropic Hardening (MISO)
- Nonlinear Isotropic Hardening (NLISO)
- Bilinear Kinematic Hardening (BKIN)
- Multilinear Kinematic Hardening (MKIN)
- Chaboche Kinematic Hardening (CHAB)
- Hill Yield Criterion (HILL)
It will help if we create a chart to understand some of the commonly used terms and how they relate to each other.
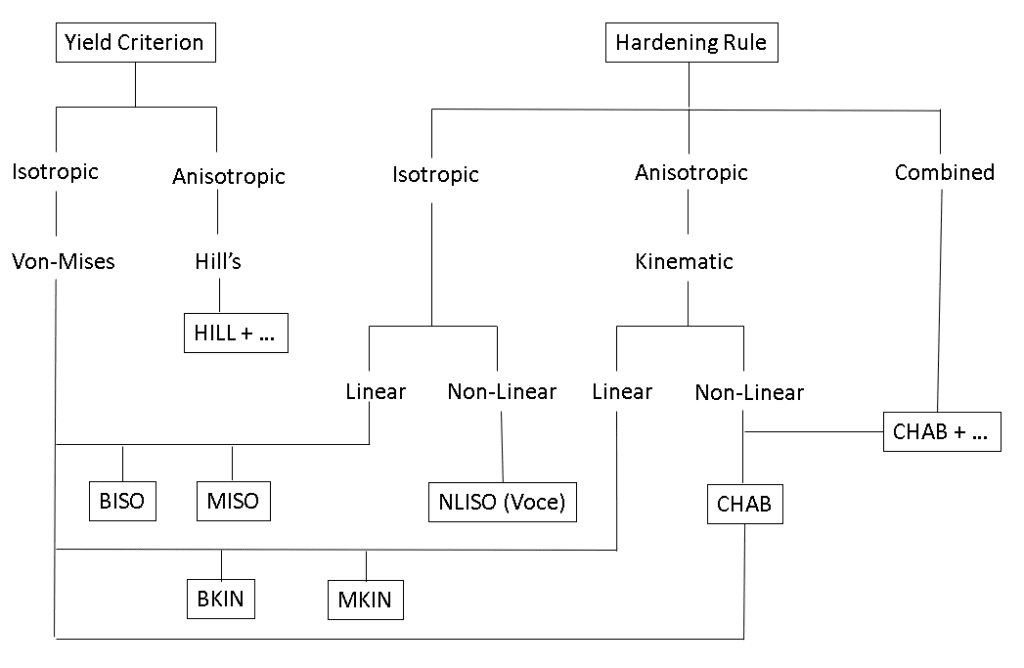
Note that the terms Isotropic and Anisotropic can be used to describe Yield Criteria or Hardening Rules. Also, von-Mises Yield criterion is the standard criterion for the most commonly used plasticity models. The Hill and Chaboche models can be used to modify various aspects of the isotropic and kinematic hardening models.
Isotropic vs Kinematic Hardening
Isotropic and kinematic hardening are two of the most commonly utilized plasticity models for ductile metals. As shown in Figure 2, kinematic hardening predicts a lower compressive yield strength than that for isotropic hardening. This (high tensile yield strength at the expense of lower compressive yield) is due to the Bauschinger effect.

Figure 3 shows the hardening rules associated with kinematic and isotropic hardening. Stress states (in terms of maximum and minimum principal stresses) that lie outside the yield surfaces will result in yielding. The dashed outline represents the shifting of the yield surface due to work hardening. The yield surface dilates, or expands uniformly for isotropic hardening whereas it translates as a rigid body for kinematic hardening.

Bilinear vs Multilinear Hardening
The “Linear” refer to the fact that there is a linear relationship between hardening and plastic strains. As can be seen in Figure 3, the dilation and translation of the yield surfaces are linearly related to the plastic strains. Also, the yield surface can flow indefinitely without any limit to its extent.
Check out FEA Tips eBook – All Models are Wrong
The “Bi” and “Multi” refer to the number of slopes that are present in the stress strain curve. A bilinear curve consists of two slopes. A multilinear stress-strain curve has more than two slopes. A smooth curve generated from multiple data points is also considered multilinear.
Non-Linear Hardening
- The relationship between hardening and plastic strains is not linear
- The yield surface cannot translate indefinitely in principal stress space
- The behavior of the model eventually reaches perfectly plastic
Which Plasticity Model to Pick?
The choice of the plasticity model depends on the material type and loading situations. The following are some guideline regarding the use of the various models:
- Isotropic hardening is suitable for large strain, proportional loading situations. Proportional loading refers to loading scenarios when the orientation of the principal stresses does not change during the course of loading
- Isotropic hardening is NOT suitable for cyclic loading applications.
- Voce Non-Linear Isotropic hardening is suitable for materials which exhibit a smooth transition between the elastic and large-strain plastic regions.
- Bilinear hardening is suitable for relatively low strain level situations (5-10% strain).
- Bilinear models do not accurately represent actual behavior accurately because the hardening is represented by a single tangent modulus (slope of line for the plastic portion of curve) and is constant.
- Multi-Linear and Non-Linear kinematic hardening are suitable for large strain scenarios.
References
[1] Advanced Mechanics Of Materials, Boresi, Schmidt, 6th edition, Page 114
[2] ANSYS Theory Manual Version 18.2, Section 4.2, Rate-Independent Plasticity
