Introduction
When we talk about mechanics of materials we refer to the relations between load and stress or between load and displacement for a system or components (members) of a system. For a given system, the load-stress relations are determined based on three factors:
- Newton’s Second Law: The equations of equilibrium or equations of motion
- The compatibility (continuity) conditions: Deformed volume elements are continuously connected without overlap or tearing.
- The constitutive relations: The observed physical response of a material under given conditions
It is instructive to discuss these principles further.
Newton’s Second Law of Motion
Newton’s laws are the foundation of classical mechanics. Classical mechanics describes the motion of macroscopic objects simplified as discrete (point) masses, travelling at speeds that are much less than the speed of light. Additionally, time and space are considered absolute (space is distinct from body and time is independent of space and events).
The differential equations of motion developed in cartesian coordinates for infinitesimal 3-Dimensional element are shown below. Bx, By and Bz represent body forces in x, y, and z axis and represent entities such as gravitational forces, electromagnetic forces or pore pressure gradients. The unit of body forces is force / volume which is consistent with the unit of stress per unit length.
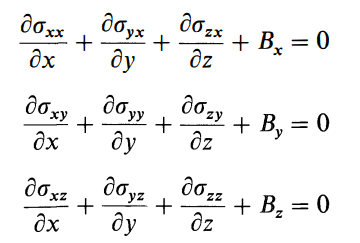
Rotational symmetry implies that shear stresses on opposing faces are equal in magnitude (σij = σji). This reduces the 9 stress terms to 6. For static structural analysis we can represent equilibrium equations by the sum of forces and moments in the three axis being equal to zero:
Σ Fx = 0 Σ Fy = 0 Σ Fz = 0
Σ Mx = 0 Σ My = 0 Σ Mz = 0
Compatibility Condition
The assumption of matter being a continuous entity is the foundation of continuum mechanics. The compatibility equations are based on this assumption. In reality, matter is not continuous. There are empty spaces within matter (how much of matter is empty space is debatable and various theories attempt to answer this question).
In structural analysis, displacements are often represented by normal and shear strains. The compatibility condition is satisfied by what we call the strain compatibility equations of small-displacement theory and is described by six equations as follows. For a derivation of these equations, refer to Boresi and Schmidt, Advanced Mechanics of Materials 6th Edition.

Constitutive Relations
The constitutive relations are developed for two reasons:
- To introduce material dependence (material properties must play a role in the force-displacement response)
- To determine solutions for systems where the number of unknowns are more than the number of equations (The compatibility equations also serve this purpose for statically indeterminate systems).
In structural analysis, constitutive relations are often referred to as material models. Here is a video by ANSYS on a basic introduction to constitutive models.
Put simply, when a force is applied on a specimen, its displacement response will vary based on the material properties. This response can be observed empirically and mathematical models can be developed to approximate these responses. Typical constitutive models are based on stress-strain relationships.
In its simplest form, a constitutive relationship exhibits linear elasticity and is described by Hooke’s law. Other material models include Hyper-elasticity, Viscoelasticity and Plasticity. You can read about an explanation of various plasticity models here.
