It is common practice to approximate behavior of structural components as springs. We see “springs” everywhere in the studies of mechanics of materials, structural dynamics, and structural analysis. Most of these springs are modeled as “Linear springs”. However, springs may be broadly categorized in three categories: Soft, Hard and Linear.
Figure 1 shows a Force displacement plot for a simple mass-spring oscillator.
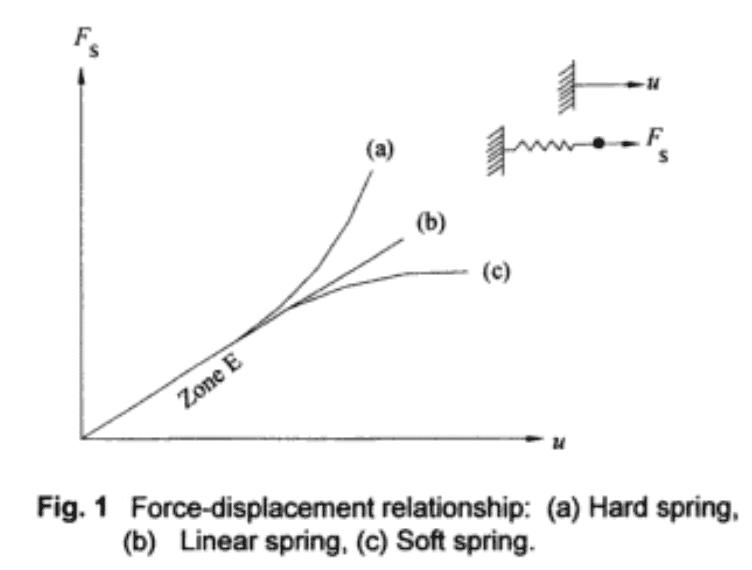
Curve (a) represents the behavior of a hard spring. The spring stiffness increases after a certain spring displacement. The force required to produce a given displacement becomes increasingly greater as the spring is deformed.
Curve (b) shows the response of a linear spring. The force required to produce a given displacement remains constant regardless of the spring displacement.
Curve (C) is designated as a soft spring. The incremental force required to produce additional displacement reduces as spring displacement increases.
Some other things of note:
- For small displacements, all three spring behaviors can be approximated as linear. This is labeled as Zone E in Figure 1.
- Linear spring approximation is common for engineering problems. This is due to one or more of the following reasons:
- The displacements of interest fall in the “small displacement” category
- The behavior of interest is most accurately represented by that of a linear spring (even at large displacements)
- Linear springs are easy to treat mathematically
- The slope of the curve is the spring stiffness (Hooke’s Law : F = Ku)
Note that soft springs should not be confused with weak springs which are employed in some structural analysis software such as ANSYS. Here, weak springs are linear springs with spring stiffness which is much lower that the overall stiffness of the system being studied. You can read more about weak springs here.
