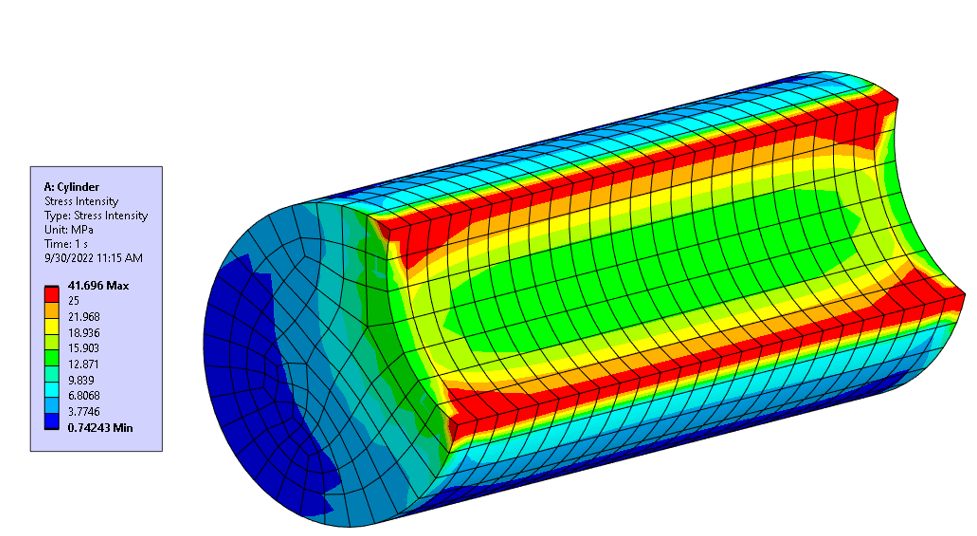
Stress concentration factor and stress intensity factor are two entirely different entities. In this article we will briefly discuss what these are and how they are different.
What is a stress concentration?
A stress concentration is a location in a component where the stress is much larger than the stress in the surrounding material.
“The conditions that cause the stresses to be greater than those given by the ordinary stress equations of mechanics of materials are called discontinuities or stress raisers. These discontinuities cause sudden increases in the stress (stress peaks) at points near the stress raisers.
The term stress gradient is used to indicate the rate of increase of stress as a stress raiser is approached. The stress gradient may have an influence on the damaging effect of the peak value of the stress. Often, large stresses due to discontinuities are developed in only a small portion of a member. Hence, these stresses are called localized stresses or simply stress concentrations.”[1]
The stress concentration factor associated with a part’s specific geometry and loading condition can be derived through experimentation, analysis or computational methods.
What is a stress concentration factor?
A stress concentration factor, is simply the ratio of the highest stress in a component to a nominal reference stress. The highest stress is typically at a stress concentration, and the nominal stress is what the stress would be if the stress raiser were not there.
Stress concentration factors are function of part geometry and loading. They can be determined experimentally, analytically or through numerical methods.
Also read, fatigue stress concentration factor.
What is a stress intensity factor?
Stress intensity factor is a concept utilized in fracture mechanics theory. Note that Stress Intensity factor has nothing to do with the equivalent stress quantity, stress Intensity (Tresca Stress).
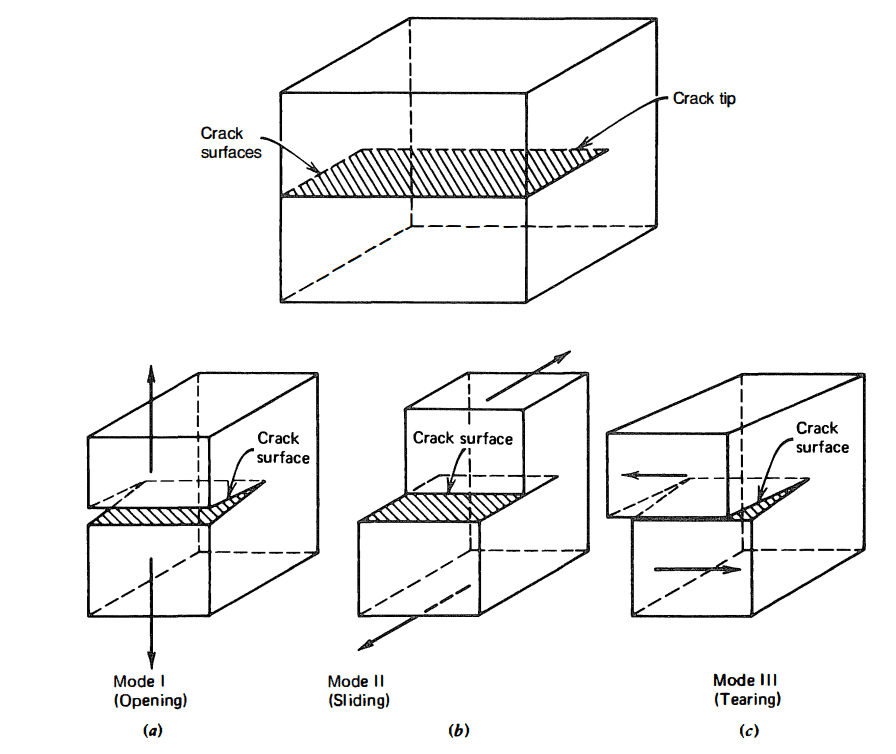
Elastic stress analysis of cracks leads to the concept of stress intensity factor K, which is employed to describe the elastic stress field surrounding the crack tip. As noted above, the motion of crack surfaces can be divided into three types, with corresponding stress fields. Hence, three stress intensity factors KI , KII , and KIII are employed to characterize the stress fields for these three modes. The dimensions of stress intensity factor K are [stress] x [length]^1/2.
The factor K depends on specimen dimensions and loading conditions. In general, K is proportional to [average stress] x [crack length]^1/2.
When K is known for a given mode (say, K1), stresses and displacements in the neighborhood of the crack
tip can be calculated.
What is a Stress Intensification Factor (SIF)?
The stress intensity factor defined above should not be confused with the stress intensification factor which is an entirely different, unrelated entity.
Stress intensification factors are fatigue correlation factors that compare the fatigue life of piping components to that of girth butt welds in straight pipe subjected to bending moments. You can read more about Stress intensification factors in this paper.
What about Stress Singularities?
Stress singularity is yet another term which is commonly used by engineers and analysts. A stress singularity has nothing to do with any of what we have discussed in this article so far. While everything discussed above is based on real phenomena, a stress singularity is nothing but a numerical artifact. It is not a “real” stress.
A stress singularity is a point in a finite element model where the value of stress does not converge to a point. The stress at a stress singularity is theoretically infinite. This may occur at nodes where point loads are applied or at boundary conditions.
Stress singularities are typically ignored when studying the behavior of structures. However, the analyst should be careful, and verify that the stress singularity does not affect the stresses in the area of interest in the model – In other words, any stress singularities must lie far from the areas of interest so as to have minimal or negligible impact on the stresses and strains of the regions of the geometry which are under study.
[1] Advanced Mechanics of Materials 5th ed., Boresi and Schmidt