What is Dynamic Amplification Factor

Dynamic Amplification Factor (DAF) is a dimensionless ratio. It represents how much a structural response to a static load magnifies, if the load were applied dynamically. The response is typically a specified displacement or stress value.

A static load does not change with time, or changes so slowly that the inertial effects are negligible. In real life, all loads are “dynamic”, but many engineering problems can be simplified to static systems with static loads. You can read more about static vs dynamic analysis here.

In some cases however, the “dynamic to static” simplification may be associated with a significant change in structural response due to the momentum, kinetic energy and damping not being represented in the static analysis. To account for this difference, the static load or its response can be multiplied by the DAF.

How is Dynamic Amplification Factor Calculated

For a Single Degree of Freedom (SDOF) system the DAF can be defined as [1]:

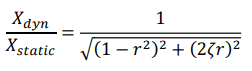
where :

r = f / fn = Ratio of the forcing frequency (applied load frequency) to the natural frequency of the structure
ζ = Zeta = Critical damping ratio (Ratio of system damping to critical damping)

If damping is ignored, the expression simplifies to:

The derivation of the DAF can be found in any elementary text on dynamics of structures.

The following plot shows the relationship between the frequency ratio and the DAF:

A couple observations can be made:

• Frequency ratio of 1 represents resonance. For an undamped system, the dynamic amplification factor at resonance is infinite.
• The amplification factor can be less than one for high frequency ratios. This is why the DAF is sometimes better referred to as Dynamic Load factor, or Dynamic Response Factor.

Dynamic Amplification factor for a Pulse Load

It should be noted that we have seen so far relates to dynamic systems with steady state harmonic loading.

If the dynamic load is a pulse, i.e. a step load, then we have a special case where the DAF for a SDOF is limited to 2.0

The derivation for the above can be found in chapter 4 of the reference. For an excellent explanation, you may refer to these Impulsive loads lecture notes by Professor Jerome Lynch of University of Michigan.

The following shows a comparison of the DAF between rectangular and triangular impulsive loads:

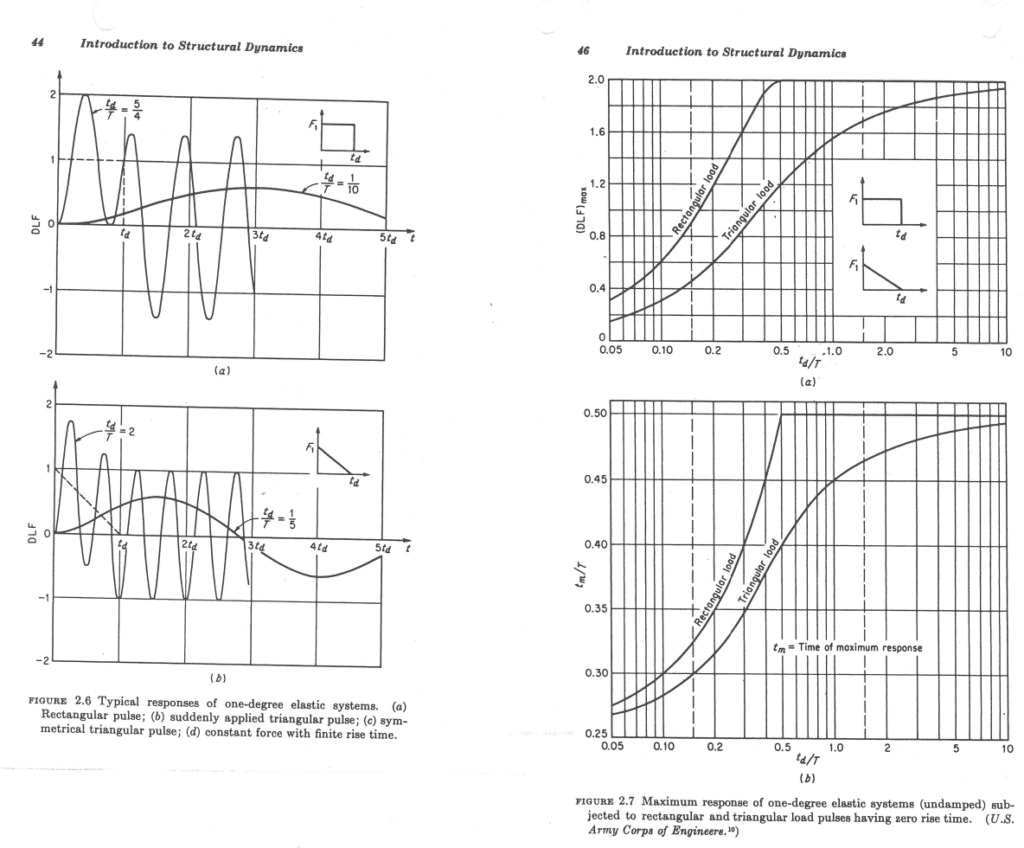
[1] RISA-3D – Dynamics Training Manual
[2] Reliability and Design of Mechanical Systems, Sengwood Woo
[3] Dynamics and Structures, Theory and Application to Earthquake Engineering, AK Chopra
[4] Introduction to Structural Dynamics, John Biggs