Introduction

In this article we will discuss some aspects of linear and non-linear analysis as they apply to structural FEA. We will also suggest when to prefer one method over the other. The article provides significant background on non-linearity and its types. The reader who is familiar with these aspects, may prefer to skip these sections and go straight to the last heading in this article (“So how to decide when to run Non-Linear FEA?”)

What is non-linearity?

We will provide the mathematical definition of non-linearity here.

A function f(x1,x2,…,xn) is linear if,

f(ax) = a f(x) and

f(x+y) = f(x) + f(y)

A non-linear system will violate one or both of these conditions.

Linear vs Non-Linear Relationships

Linear and non-linear are terms which may be used to describe a broad spectrum of mathematical expressions or numerical models. More precisely, whenever a mathematical relationship exits between two parameters, the nature of the relationship may be described as linear or non-linear.

A relationship between two parameters x and y is linear, if it can be described as follows:

y(x) = mx + c

where m and c are constants, and y does not depend on x (i.e. the mathematical conditions for linearity mentioned earlier are met).

You will recognize the above expression as the equation of a line with slope m and y-intercept c.

If x and y can not be described as above, then the relationship is termed non-linear.

Most relationships that exist in nature are non-linear

In general, the mathematics with which we model and understand our world is quite complex. We observe that natural phenomena are mostly governed by non-linear relationships. Having said this, it is common for scientists and engineers to assume linear relationships for a vast spectrum of physical problems. This is mainly because a system of linear equations is easy to solve, and often presents a solution which is sufficiently accurate.

Linear vs Non-Linear FEA

The underlying equation for structural FEA is {F}= [K]*{X}

Where {F} is the input load vector and [K] is the global stiffness matrix. {X} is the unknown displacement vector which is solved for at each mesh node (What is a node?) in the model.

You can recognize this equation as a representation of Hooke’s law.

A structural analysis is linear as long as [K] and {F} are not functions of {X}.

The assumption in a linear analysis is that the stiffness of the structure is a function of its original shape and nothing else. A change in the structure’s shape caused by deformations does not have a significant impact on the stiffness (and so is ignored).

Additionally, the applied load is also assumed to be independent of the displacements within the model.

Why would the stiffness of a structure NOT be constant?

This question can essentially be rephrased as, What are the sources of non-linearity in a structural FEA?

Let us attempt to answer this question.

The stiffness of a structure is a function of its geometry, interactions (between surfaces of a component or multiple components) , and material properties (For a beam of length L, cross section Area A, and Young’s Modulus E, the stiffness in the direction of L, may be computed as, K = AE/L).

More precisely, there are three sources of non-linearity in a structural analysis:

1- Geometric Non-Linearity

Geometric non-linearity is of two types:

• Deformations:
  Geometric Nonlinearity arises when deformations are large enough to alter the distribution or orientation of applied loads, or the orientation of internal resisting forces and moments. Relevant examples include elastic contact in a roller bearing, where contact pressure is spread over an increasing area as load increases, and a vaulter’s pole which resists load mainly with P/A stress or mainly with My/I stress directed tangent to the pole, depending on whether it is almost straight or is severely bent. Note that geometric nonlinearity may not involve “large displacements” (relative to the smallest dimension of the structure). In the elastic contact problem, displacements are small [1]. The essential difficulty of nonlinear analysis is that the stiffness matrix is a function of, and must be computed with respect to the deformed geometry – which is not known in advance.
  
  
• Stress Stiffening:
  Stress stiffening (also called geometric stiffening, incremental stiffening, initial stress stiffening, or differential stiffening by other authors) is the stiffening (or weakening) of a structure due to its stress state. This stiffening effect normally needs to be considered for thin structures with bending stiffness very small compared to axial stiffness, such as cables, thin beams, and shells and couples the in-plane and transverse displacements [2].
  
  In ANSYS, Geometric Non-Linearity can be activated by turning on “Large deflections” under the solver control settings.

2- Contact Non-Linearity

This is also referred to as Changing-Status Non-Linearity. Many common structural features exhibit nonlinear behavior that is status dependent. When the status of a physical system changes, its stiffness shifts abruptly [3]. In ANSYS, a contact interface can have an open (gap) status or closed (touching) status.

The contact problem is a kind of geometrically nonlinear problem that arises when different structures, or different surfaces of a single structure, either come into contact or separate or slide on one another with friction. Contact forces, either gained or lost, must be determined in order to calculate structural behavior. The location and extent of contact may not be known in advance, and must be determined. Usually, friction between contacting surfaces must be taken into account. Sometimes a flow of heat or electric current takes place at a contact, and may have to be represented because it influences structural behavior [1].

In ANSYS, Bonded and No Separation contacts are linear contacts (because they remain closed). Rough, Frictional and Frictionless contacts are non-linear (since they allow opening and closing or gap vs in-contact states).

3 – Material Non-Linearity

The image below shows a typical stress-strain curve of a ductile material (low carbon steel).

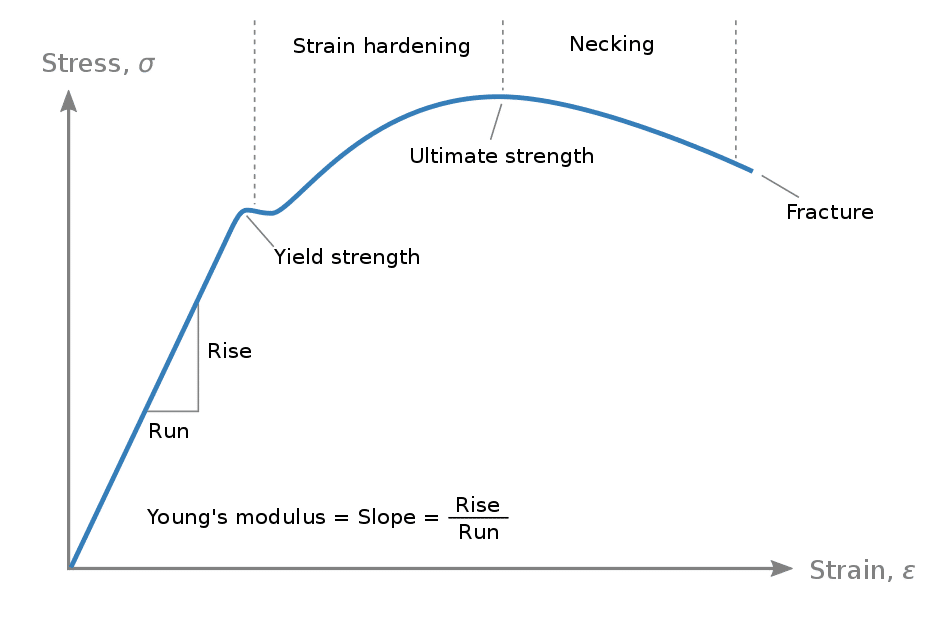
The Stress-Strain response of this material is linear up to its yield point, after which it enters the realm of plasticity, or material non-linearity. Loads that cause a material to yield result in plastic strains which must be modelled using material plasticity models.

In ANSYS workbench material non-linearity can be accounted for by inputting a stress-strain curve. Note that, even with the material curve defined, plasticity will only come into play once the structure is stressed beyond its elastic limit. The equivalent command in ANSYS APDL is NLGEOM, ON

So how to decide when to run non-linear FEA?

Now that we have an understanding of what non-linearity is, and how it applies to structural analysis, we are in a good position to answer this question. The obvious (but comprehensive) answer to this question is:

A non-linear FEA should be performed whenever a linear analysis is not expected to provide a solution which is sufficiently accurate.

However, determining what is “sufficiently accurate” typically requires some degrees of knowledge, skill and experience. Sometimes, only one of the three non-linearities may need to be activated (for example frictional contact with linear-elastic material properties and large deflections turned off). Other times you may want to include all three non-linearities.

Having said this, below we will list some guidelines and considerations which could assist an analyst in making this call.

1. Run Linear FEA as a “first pass” analysis:
   
   It is a good practice, especially when dealing with large assemblies to start with linear FEA. It is not uncommon for experienced analysts to initially assess a complex system by running it as a purely non-linear analysis. Once they get a solution as expected, they may incrementally introduce the various non-linearities in subsequent runs. Linearities, especially material non-linearity is computationally expensive (requires advanced hardware and takes longer to run) and is often numerically challenging (difficult to converge to a solution).
   
   
2. Run Linear FEA as a debugging tool:
   
   This is especially true when a model with non-linear contacts fails to converge. Changing the contacts to bonded or No Separation may aid in convergence and help identify areas of the model requiring tweaks or improvements.
   
   
3. Consult internal design and analysis guidelines:
   
   If you work for an organization that uses FEA as a tool for product research and design, chances are that you have to abide by design codes and guidelines. The internal guidelines may refer to external standards maintained by ASME / ISO / ASTM etc. These guidelines will typically provide specific instructions or recommendations for analysis. As an analyst you may have to adhere to these instructions (for example, linear-elastic analysis may be allowed in some situations but not in others). In some ways, this makes your life easier as you don’t have to decide what route to choose. But in other cases, experienced analysts can challenge the guidelines and deviate from them as long as they can provide the justifications for it.
   
   
4. Consider what role plasticity may play in the design:
   
   Some designs are such that they can not tolerate any plasticity. By tolerate, we mean that plastic strains are undesirable and must be avoided. For example, a component made of a brittle material (glass or graphite for example) will not develop appreciable plastic strains before fracturing. It is typically meaningless to run an elastic-plastic analysis to study the structural response of a brittle material.
   
   On the other end of the spectrum are scenarios where plasticity is a desirable feature. One relevant example is metallic seals which seal by way of plastic deformations. Another example is metal forming operations where components may undergo manufacturing processes (such as rolling, bending) to achieve particular shapes, or enhanced strengths due to work hardening. Modeling such phenomena would absolutely require that an elastic-plastic analysis be performed.
   
   However, most real world designs featuring ductile metallic components allow some degree of plasticity. For example, local plastic strains that develop at contact interfaces (such as between a pin and a hole), at geometric features that act as stress raisers (fillet, radii) or even at the roots of threads. In many instances, small amounts of local plasticity has little to no effect on the form, fit, function and aesthetics of a component.
   
   A linear elastic analysis can often be conservatively used to verify that a design is protected against plastic failure (such as collapse, rupture or progressive increase in plastic strains leading to excessive deformations). One can do this by limiting the maximum stress to stay below yielding, or look into stress linearization. But there are situations when linear-elastic analysis is not sufficient. These are discussed in the next point.
   
   
5. Non Linear elastic-plastic analysis is typically desirable when:
   
   Plasticity is a design feature: This has been mentioned earlier – Metallic seals, metal forming operations, mechanisms where plasticity is employed (certain types of locking mechanisms).
   
   Linear elastic analysis cannot confirm protection against failure due to plasticity: An elastic-plastic (EP) analysis (when performed appropriately) can predict the system response at high loads with a great degree of accuracy and confidence. Many design that would “fail” according to linear elastic analysis end up “passing” when checked against elastic-plastic criteria. As long as the skill of the analyst, hardware resources, and time allotted for the project permit, an EP analysis can be an invaluable tool for design qualification.
   
   A high degree of design optimization is to be performed: Often times, certain constrains are imposed on the design which necessitate the use of elastic-plastic analysis. For example, budget, aesthetics or assembly constrains may demand that a part be limited to a certain size or weight. If you are asked to fine tweak a design to determine its optimal version, a linear elastic analysis may not be sufficient. An elastic-plastic analysis could act as the fine tipped pencil with which the most optimized and efficient design can be drawn.
   
   
6. Non-Linear geometry and material non-linearity usually co-exist:
   
   It is worth mentioning that if you are running an elastic-plastic analysis it makes a lot of sense to account for Non-linear geometry. In many cases, leaving it off would not only lead to inaccurate results, but may also cause severe convergence difficulties. Large plastic strains are associated with large strains (deformations) which makes it self explanatory to activate non-linear geometry effects.
   

References

[1] Concepts and Applications of Finite Element Analysis, 4th Ed, Robert Cook
[2] ANSYS Theory Manual Section 3.4
[3] The Finite Element Method and Applications in Engineering Using ANSYS, Edrogan Madenci
[4] Wikipedia, Stress-Strain Curve