When a force is exerted perpendicular to a surface, it induces a normal stress. Normal stress can be compressive or tensile.
From Mechanics of Materials 7th edition, James Gere:
In general, the stresses s acting on a plane surface may be uniform throughout the area or may vary in intensity from one point to another. Let us assume that the stresses acting on cross section mn.
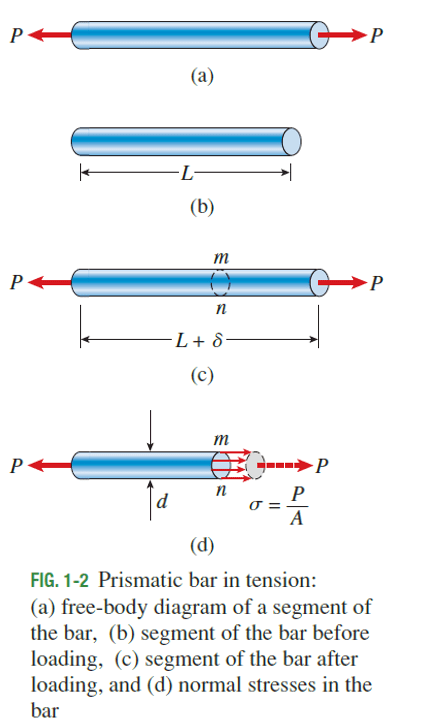
(Fig. 1-2d) are uniformly distributed over the area. Then the resultant of those stresses must be equal to the magnitude of the stress times the cross-sectional area A of the bar, that is
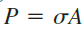
Therefore, we obtain the following expression for the magnitude of the stresses:
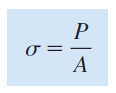
This equation gives the intensity of uniform stress in an axially loaded, prismatic bar of arbitrary cross-sectional shape. When the bar is stretched by the forces P, the stresses are tensile stresses; if the forces are reversed in direction, causing the bar to be compressed, we obtain compressive stresses. Inasmuch as the stresses act in a direction perpendicular to the cut surface, they are called normal stresses. Thus, normal stresses may be either tensile or compressive.
This page is part of The Encyclopedia of Stresses in Solids