1) The underlying equation for structural FEA is {F}= [K]*{X}
Where {F} is the input load vector and [K] is the global stiffness matrix. {X} is the unknown displacement vector which is solved for at each node in the model.
2) The above gives displacement results only at the nodes. There is no information yet on how the points inside the element (which are not defined in the mesh) deflect. The solver interpolates the nodal displacements at these points by solving a “shape function”. Which function is used depends on the element type.
3) Unlike forces, stresses and strains are not computed at the nodes. They are computed at specific “integration points” within the element. See below for an example of an element with 8 nodes.
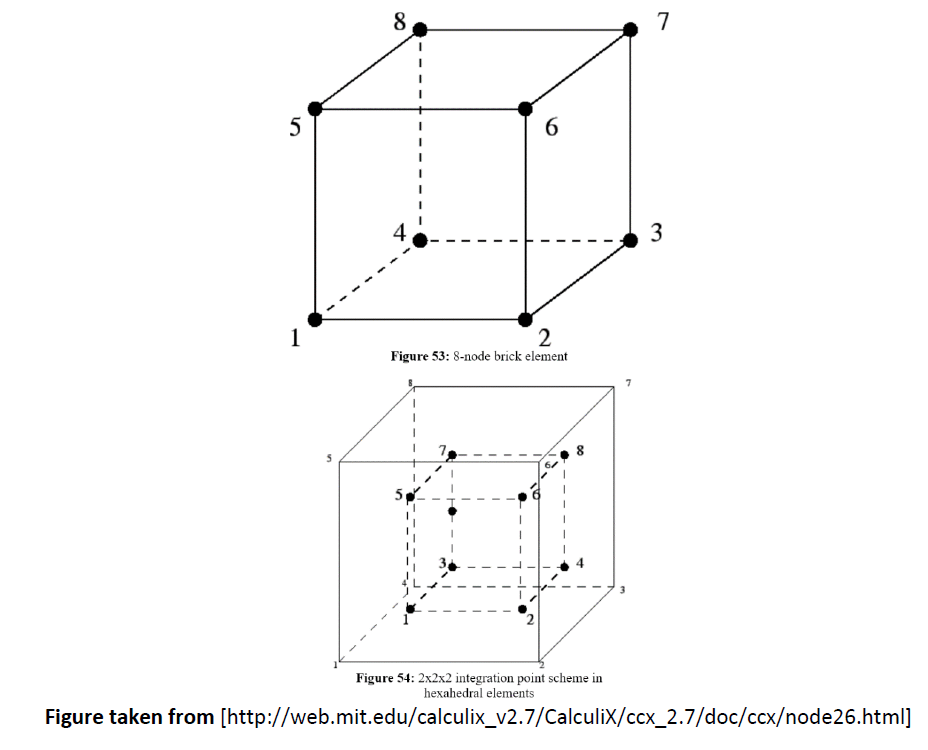
4) The equation used to calculate stresses is {σ} = [D]*{ε} Where [D] is the elasticity matrix containing material properties information.
5) Once the stresses / strains have been computed, they are extrapolated out to the nodes and averaged across the element.
6) Refining the mesh has the effect of softening the model due to better discretization of the geometry. Therefore, (assuming everything else remains constant), a refined mesh will usually result in higher displacements, strains, and stresses.
7) In some cases, a coarse mesh may generate inaccurately higher stresses than a refined mesh. This is usually due to a combination of the errors introduced in step (2) (interpolation of nodal displacements within the element – i.e. model is too stiff) and step (6) (extrapolation of stress results to nodes and averaging across the element – i.e. there are too few integration points).