Bending stress is a normal stress that is induced on a structure by a bending moment.
The following is taken from Mechanics of Materials 7th Edition by James Gere.
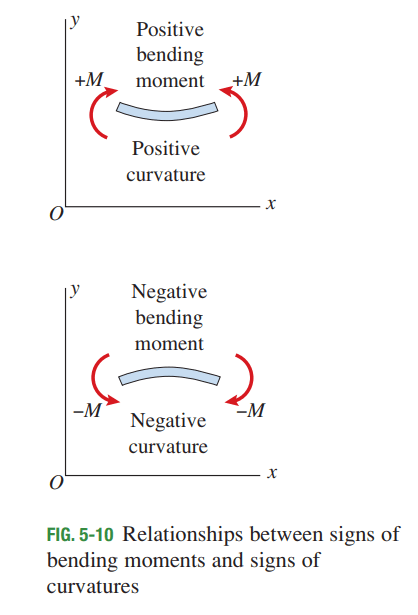
Consider a beam as shown in the figure above. The beam has an area moment of Inertia I and is subjected to a bending moment M. The stress at any point along the y-direction in the beam is given by :
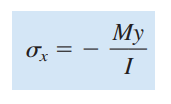
This equation, called the flexure formula, shows that the stresses are directly proportional to the bending moment M and inversely proportional to the moment of inertia I of the cross section. Also, the stresses
vary linearly with the distance y from the neutral axis, as previously observed. Stresses calculated from the flexure formula are called bending stresses or flexural stresses.
If the bending moment in the beam is positive, the bending stresses will be positive (tension) over the part of the cross section where y is negative, that is, over the lower part of the beam. The stresses in the upper
part of the beam will be negative (compression). If the bending moment is negative, the stresses will be reversed.
This page is part of The Encyclopedia of Stresses in Solids