The Cauchy stress tensor is a nine component symmetric tensor which describes the stress state of a 3D stress element at any point in a structure. Consider the stress element shown below:

The stress state for this element is described as:
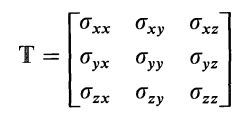
The following is an excerpt from Mechanics of Materials 7th Edition, by James Gere:
Augustin Louis Cauchy (1789–1857) was one of the greatest mathematicians. Born in Paris, he entered the
École Polytechnique at the age of 16, where he studied under Lagrange, Laplace, Fourier, and Poisson. He was quickly recognized for his mathematical prowess, and at age 27 he became a professor at the École and a member of the Academy of Sciences. His major works in pure mathematics were in group theory, number theory, series, integration, differential equations, and analytical functions.
In applied mathematics, Cauchy introduced the concept of stress as we know it today, developed the equations of theory of elasticity, and introduced the notion of principal stresses and principal strains.
This page is part of The Encyclopedia of Stresses in Solids